Suppose we have four Schweizer SGS 1-26 gliders, identical except for color. For our test, we will line them up and fly them at the speeds and sink rates in the following table:

Glider
Airspeed	26 Knots	31 Knots	42 Knots	62 Knots
Sink Rate	1.8 Knots	1.6 Knots	1.9 Knots	3.2 Knots

If the four gliders start together and proceed in the same direction at their respective speeds and sink rates, a side view will look like this. After one minute, their positions relative to their starting points will be shown by the distance graph (for simplicity we will let one knot = 100 feet per minute - the error is trivial). That means that the blue glider has flown 2600 feet horizontally and 180 feet vertically. Similarly, the green glider has flown 3100' horizontally and 160' vertically, the yellow glider 4200' horizontally and 190' vertically, and the red glider 6200' horizontally and 320' vertically.

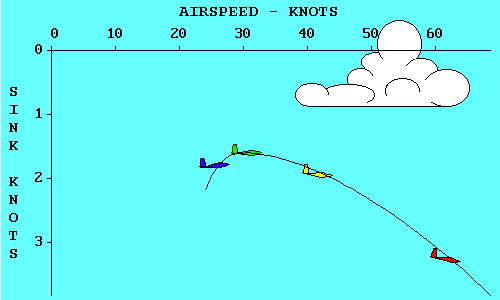Now if we connect the gliders with a smooth curve and change the distance scales to speed scales, we have just drawn a polar curve for the Schweizer SGS 1-26.

Lets pretend we started this exercise with the gliders 320 feet above the ground. The red glider is already touching down (actually crashing because we didn't allow any room for a flare). If we continue the descent of the other gliders until the blue and yellow gliders also reach the surface, we see several things. First, the yellow glider goes farther than any other while losing 320 feet. The blue glider touched down about the same time, but doesn't go nearly as far. The green glider is still in the air, but will crash on top of the red glider if it isn't moved quickly.

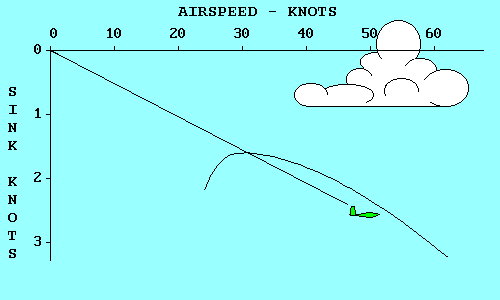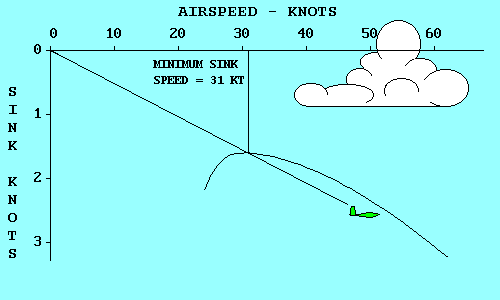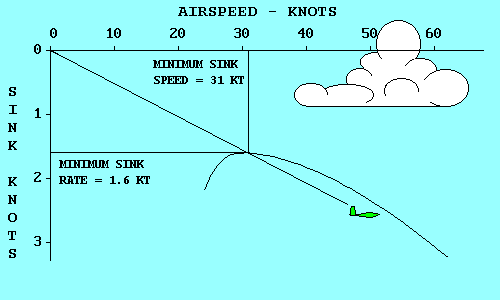The green glider has the lowest sink rate of any. It will keep you in the air for the longest time, but will not go very far. Note that its glide path intersects the polar curve at its highest point. If we move up from the highest point on the polar curve to the airspeed scale we find that the minimum sink speed for a SGS 1-26 is 31 knots (35 mph). If we move horizontally to the left we find that the minimum sink rate is 1.6 knots (160 feet per minute).

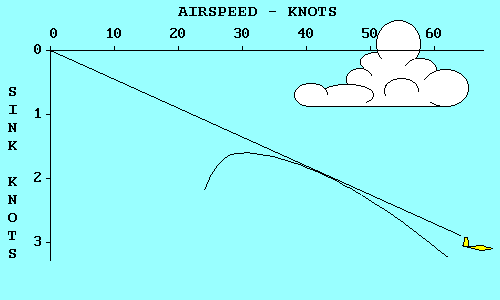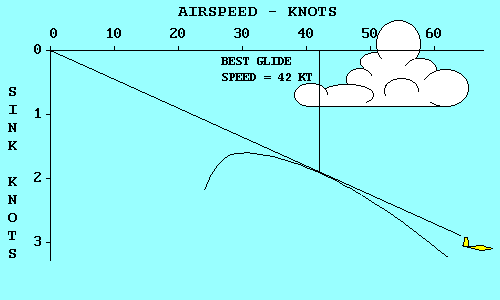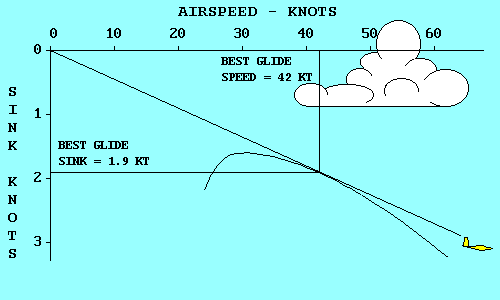The yellow glider has the best glide ratio of all. That means that it will glide farther in still air than any other glider, for a given loss of altitude. A line from the origin (0, 0 point) of the graph, that is tangent to (just touches) the polar curve represents the glide path of the yellow glider. If we move up from the point where the line touches the polar curve to the airspeed scale, we find that the speed that produces this best glide is 42 knots (48 mph). If we move horizontally to the left from the tangent point we find the corresponding sink rate, 1.9 knots (190 feet per minute).

To see how sinking air affects our glide let's compare the red and yellow gliders. If both enter an air mass that is sinking at 300 feet per minute (3 knots), their sink rates will increase accordingly. The yellow glider is now sinking at 4.9 kts (1.9 within the air mass plus 3 for the air mass sink rate). The red glider is now sinking at 6.2 kts (3.2 + 3.0). Both enter the air mass at the same altitude; our objective is to come out the other side with the least loss of altitude. Although the red glider is sinking faster, it is also moving horizontally much faster (62kts vs 42 kts). The result is that it gets out of the sinking air at a higher altitude than the yellow glider. The red glider has a better glide ratio, relative to the ground, than the yellow one even though the yellow glider has a better glide ratio relative to the air mass.

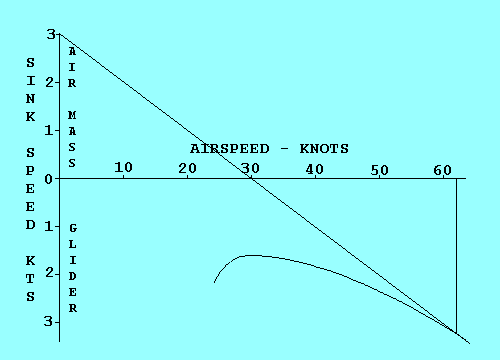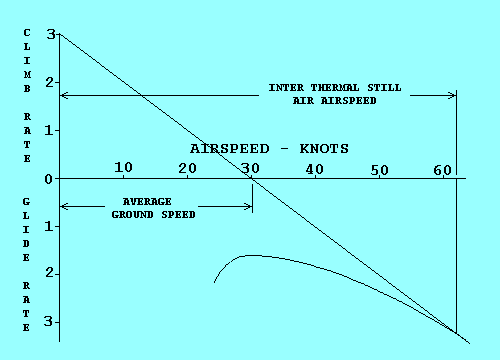
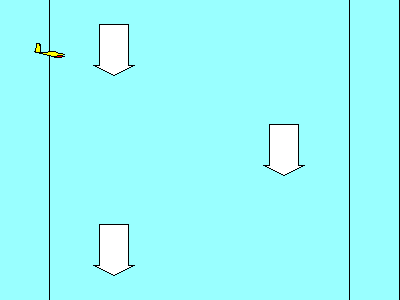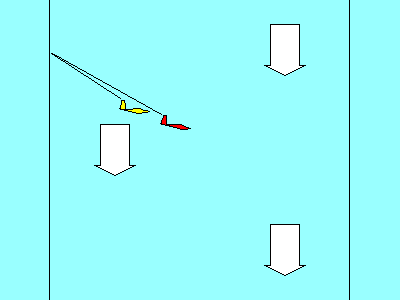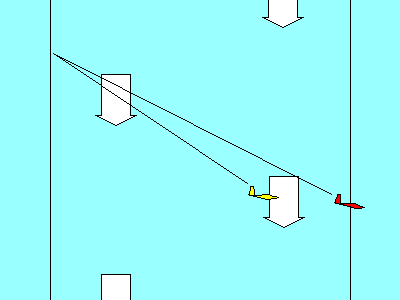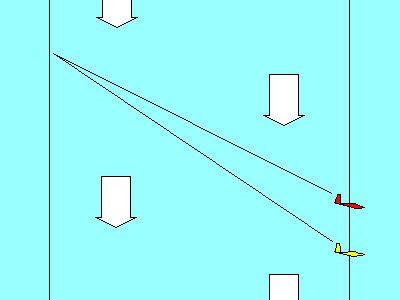
In our previous examples our polar curve showed performance relative to the air mass in which the glider was flying. It was valid relative to the ground only in still air. To be valid relative to the ground the curve must be displaced in the direction and by the amount that the air mass is moving. In this example the air is sinking at 300 feet per minute (3 kts), so we move the curve down 3 kts. To determine the Speed to Fly for any condition, we draw a line from the origin that is just tangent to the curve. Then we draw a line straight up from the tangent point to the speed scale. In this case the Speed to Fly is 62 kts. Did that surprise you?

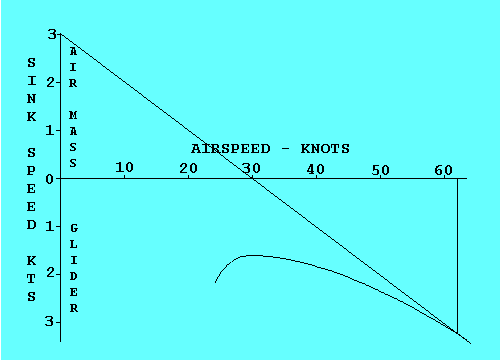An easier way to accomplish the same objective is to raise the origin of the graph by an amount equal to the air mass sink rate and then draw a tangent to the original curve from that point. To keep our examples consistent, let's assume a 3 knot air mass sink rate and move the origin up 3 knots. Now the tangent to the original curve occurs at the same 62 knots we found in the previous example. When using this method be sure to remember that the glider sink rate is the sum of its sink rate within the air mass and the sink rate of the air mass itself. In this case it is 6.2 kts (air mass sink of 3 kts plus glider sink within the air mass of 3.2 kts = 6.2 kts).

If the air is rising we displace the origin down by an amount equal to the rate at which the air is going up, and then draw a tangent from that point to the polar curve. This gives a valid speed only if we plan to fly straight through the lift. If we plan to circle in the lift, other factors determine the speed that will optimize our climb rate. For a headwind we displace the origin to the right, using the airspeed scale to determine how far we move it. For a tailwind we displace the origin to the left.

First let's discuss headwinds and tailwinds. You have to estimate their values so a rule of thumb is as good as anything. If you were to evaluate several different wind conditions graphically, you would find that the tangent point moves about half as far as the origin. Thus, a good rule would be "Add about half the estimated value of a headwind, and subtract about half the value of a tailwind from the Speed to Fly determined for lift or sink."

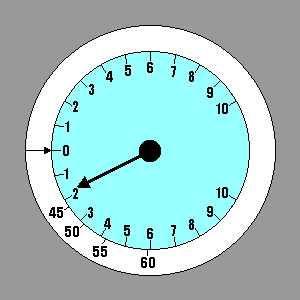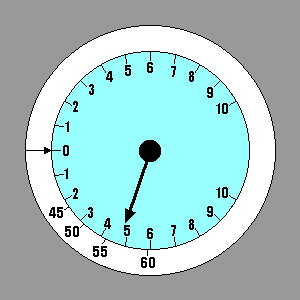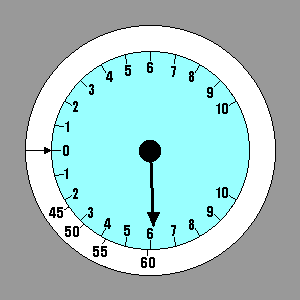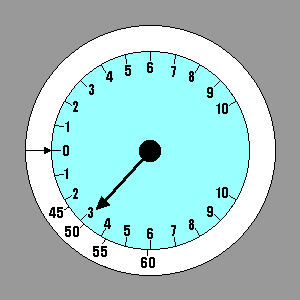For lift and sink we have an instrument in the glider to give us the necessary information. The process used to determine Speed to Fly gives us the sink rate of the air mass and the sink rate of the glider within the air mass. Their total is the value that would be indicated on the variometer. We could select a few representative values of Speed to Fly and stick them on the panel adjacent to the corresponding variometer readings, using a label maker. A better method is to invest in a speed ring for the glider/variometer combination we have. The speed ring is adjustable, but for our current definition of Speed to Fly it should be set with the arrow on the ring pointing to "0" on the variometer. Then when the variometer points to any rate of descent it is also pointing to the corresponding Speed to Fly - the one that will produce the flattest glide under those conditions. Our example shows Speed to Fly varying from 42 kts in still air to 62 kts in 3 kt sink.

Although the Speeds to Fly that we have been discussing so far are the ones that will let you glide to that safe landing spot if any will, they are too slow to win contests and too slow for most cross-country flights. In these cases we are more interested in covering the ground in the shortest time rather than obtaining the flattest glide. That introduces a new definition of Speed to Fly. Credit for developing this concept of Speed to Fly is usually given to Paul MacCready, and the speed ring discussed earlier is usually called a MacCready speed ring. Cross-country flights utilizing thermals consist of alternately climbing in one thermal and gliding to the next. MacCready noted that the Speed to Fly between thermals should be based on the strength of the thermals. If the thermals are strong you can fly faster than the speed that produces the flattest glide. You will lose more altitude, but you make up for it by climbing faster in the next thermal. Thus you reach the top of the next thermal sooner than you would have at the lower speed.

We can analyze Speed to Fly in this case by using the same technique we used for flattest glide in sinking air, except that we offset the polar curve origin by the rate of climb we expect in the next thermal instead of air mass sink rate. To illustrate the similarity we assume a climb rate of 3 kts and see that the graph is identical to the one with 3 kts sink except for the labels. It shows that the Speed to Fly between thermals in still air is 62 kts if you expect to climb at 3 kts in the next thermal. An added benefit is that the average cross-country speed, including the time spent circling in thermals, can be estimated by the point on the airspeed scale where the tangent line crosses the scale.

Some pilots might question using a climb rate in the next thermal, one that has not yet been attained, to set the speed ring. They should try to remember the last time they made a decision with complete information. In this case one could base the estimate on the climb rate in the last thermal, modified by an assessment of conditions ahead and whether they appear to be improving or deteriorating. Once set, the value selected is still subject to change. A good way to think of the MacCready setting is that it represents the minimum climb rate that the pilot is willing to stop for. As altitude decreases and the prospects of landing out increase, the prudent pilot will accept weaker thermals, and the MacCready ring should be set accordingly. A really desperate pilot should set the ring to zero to maximize the area to be searched for a thermal.

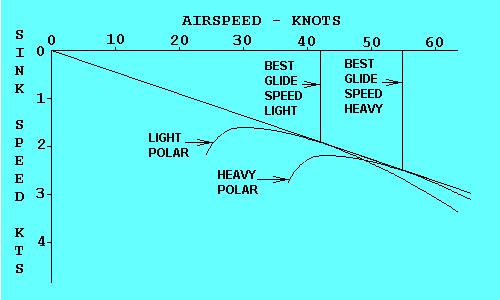A different polar curve exists for the same glider at every gross weight. As the weight increases the polar moves down and to the right and becomes a little flatter, but retains approximately the same shape. Both airspeed and sink rate increase for equivalent points on the curves, but their ratio remains the same. Both heavy and light glider achieve the same best glide ratio, as shown here, but the heavy glider does so at a higher speed. This is the reason for carrying ballast to improve glide performance when the thermals are strong enough, even though the climb rate suffers.